加速度

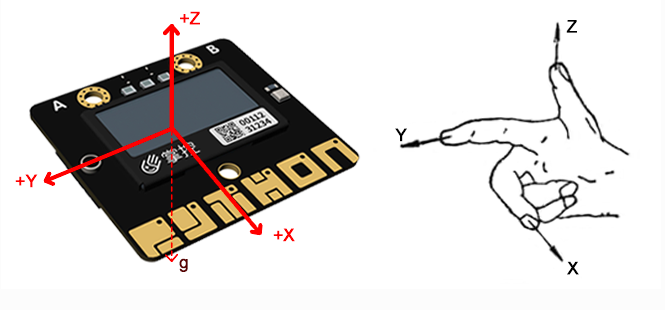
加速度传感器能够测量由于重力引起的加速度，传感器在加速过程中，通过对质量块所受惯性力的测量，利用牛顿第二定律获得加速度值。掌控板上的加速度计可测量加速度，测量范围为 -2g 到 +2g 之间。

掌控板的测量沿3个轴，每个轴的测量值是正数或负数，正轴越趋近重力加速度方向，其数值往正数方向增加，反之往负数方向减小，当读数为 0 时，表示沿着该特定轴“水平”放置。

• X - 向前和向后倾斜。
• Y - 向左和向右倾斜。
• Z - 上下翻转。

例：通过OLED显示屏来观察3个轴加速度值的变化

    from mpython import *

    while True:
        oled.fill(0)     
        x1 = accelerometer.get_x()
        y1 = accelerometer.get_y()
        z1 = accelerometer.get_z()
        oled.DispChar("加速度x:", 0, 0)
        oled.DispChar(str(x1), 48, 0)
        oled.DispChar("加速度y:", 0, 16)
        oled.DispChar(str(y1), 48, 16)
        oled.DispChar("加速度z:", 0, 32)
        oled.DispChar(str(z1), 48, 32)
        oled.show()

使用前，导入mpython模块:

    from mpython import *

获取X、Y、Z三轴的加速度:

    x1 = accelerometer.get_x()
    y1 = accelerometer.get_y()
    z1 = accelerometer.get_z()

注解： 通过 accelerometer.get_x() 获取3轴加速度。获取3轴加速度获取方法分别为 get_x() 、get_y() 、get_z() 。
每个轴的测量值根据方向是正数或负数，表示以克为单位的值。

您可以尝试掌控板按以下放置，观察3轴数据:

• 平放桌面 --(0,0,-1)
• 翻转平放桌面 --(0,0,1)
• 掌控板下板边直立与桌面 --(1,0,0)
• 掌控板左板边直立与桌面 --(0,1,0)

注解：

发现什么规律没有？当重力加速度与加速度轴方向一致时，即等于1g的地球重力加速度。正方向为+1g，反方向为-1g。
假如您猛烈地摇动掌控板，您会看到加速度达到±2g，那是因为这个加速度计的最大测量值为±2g。

水平球

from mpython import *    #导入mpython模块

Center_x=63           #设定中心点（原点）x的坐标
Center_y=31           #设定中心点（原点）y的坐标

while True:

    x=accelerometer.get_x()         #获取X轴的加速度
    y=accelerometer.get_y()         #获取Y轴的加速度

    if y<=1 and y>=-1:
        offsetX=int(numberMap(y,1,-1,-64,64))   #映射Y轴偏移值
    if x<=1 and x>=-1:
        offsetY=int(numberMap(x,1,-1,32,-32))   #映射X轴偏移值
    move_x=Center_x+offsetX                 #水平球在X坐标上的移动
    move_y=Center_y+offsetY                 #水平球在Y坐标上的移动

    oled.circle(Center_x,Center_y,6,1)      #画中心固定圆：空心
    oled.fill_circle(move_x,move_y,4,1)     #画移动的水平球：实心
    oled.DispChar("%0.1f,%0.1f" %(x,y),85,0)    #显示水平球在X、Y轴的加速度值

    if offsetX==0 and offsetY==0:
        rgb.fill((0,10,0))          #水平球在中心位置亮绿灯，亮度为10
        rgb.write()
    else:
        rgb.fill((0,0,0))           #水平球不在中心位置灭灯
        rgb.write()
    oled.show()
    oled.fill(0)

当检测到掌控板在X轴和Y轴方向倾斜时（范围-1g 至+1g），将X轴、Y轴的偏移值也就是加速度值（范围-1至1）分别映射在以设定的中心点为原点的X坐标上的Y坐标（范围32至-32）、X坐标（范围-64至64）上:

    if y<=1 and y>=-1:
        offsetX=int(numberMap(y,1,-1,-64,64))
    if x<=1 and x>=-1:
        offsetY=int(numberMap(x,1,-1,32,-32))

注解：

numberMap(inputNum, bMin, bMax, cMin, cMax) 是映射函数，``inputNum`` 为需要映射的变量，``bMin`` 为需要映射的最小值，``bMax`` 为需要映射的最大值，``cMin`` 为映射的最小值，``cMax`` 为映射的最大值。   

水平球在X、Y坐标上的移动：水平球在坐标上的移动 = 中心点位置 + 加速度的偏移值:

    move_x=Center_x+offsetX
    move_y=Center_y+offsetY 

如果水平球移动到中心位置，则亮绿灯，否则不亮灯:

    if offsetX==0 and offsetY==0:
        rgb.fill((0,10,0))          #水平球在中心位置亮绿灯，亮度为10
        rgb.write()
    else:
        rgb.fill((0,0,0))           #水平球不在中心位置灭灯
        rgb.write()

计算掌控板倾斜的角度

# 通过y轴加速度求y轴与水平面倾斜角度

from mpython import*
from math import acos,degrees

while True:
    y=accelerometer.get_y()
    if y<=1 and y>=-1:
        rad_y=acos(y)
        deg_y=90-degrees(rad_y)
        oled.DispChar('%.2f°' %deg_y,50,25)
        oled.show()
        oled.fill(0)

使用前，导入mpython模块和math模块中acos函数、degrees函数:

    from mpython import *
    from math import acos,degrees

获取X轴的加速度:

    x = accelerometer.get_x()

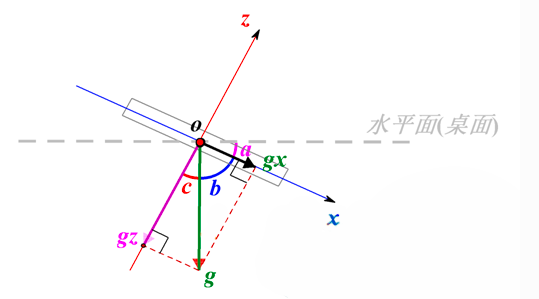
假设掌控板参考水平面为桌面，掌控板倾斜过程中，Y轴与桌面是平行，其夹角不变（一直是0度），发生变化的是X轴与桌面的夹角以及Z轴与桌面的夹角，而且桌面与X轴Z轴夹角变化度数是一样的。为了方便分析，我们从Y轴的方向俯看下去，那么这个问题就会简化成只有X轴和Z轴的二维关系。假设某一时刻掌控板处于如下状态：

在这个图中，Y轴已经简化和坐标系的原点O重合在了一起。我们来看看如何计算出掌控板的倾斜角，也就是与桌面的夹角a。g是重力加速度，gx、gz分别是g在X轴和Z轴的分量。

由于重力加速度是垂直于水平面的，得到： 角a+角b=90度 X轴与Y轴是垂直关系，得到： 角c+角b=90度 因此： 角a=角c

根据反余弦定理，计算角b的弧度值::

    rad_x=acos(x)

计算夹角的角度，即角a=角c=90度-角b::

    deg_x=90-degrees(rad_x)

注解：

* acos() 函数为返回反余弦弧度值。   
* degrees() 函数为将弧度转换为角度。